Optique – Photographie

Formules d’optique pour la photographie : relations de conjugaison, profondeur de foyer, profondeur de champ.

Relations de conjugaison

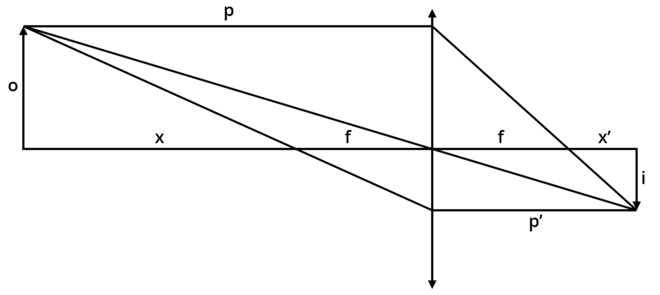
Définitions

i	Dimension de l’image
o	Dimension de l’objet
f	Distance focale
x’	Allongement, ou distance du point focal image à l’image
p’	Tirage, ou distance du centre optique à l’image
x	Distance du point focal objet à l’objet
p	Distance du centre optique à l’objet

Relation de Descartes

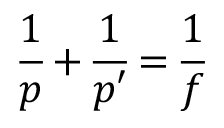
1/p + 1/p' = 1/f

Relation de Newton

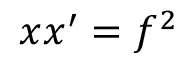
x·x' = f²

Grandissement

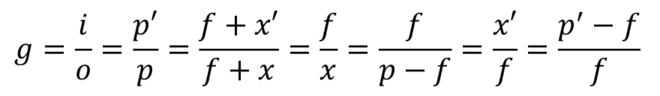
g = i/o = p'/p = (f+x')/(f+x) = f/x
  = f/(p-f) = x'/f = (p'-f)/f

Calculs

Connaissant la focale et le grandissement, on obtient :

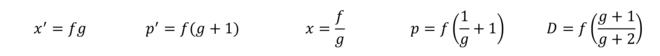
x' = f*g
p' = f*(g+1)
x  = f/g
p  = f*(1/g+1)
D  = f*(g+1/g+2)

Connaissant le grandissement et la distance de l’objet au centre optique, on obtient :

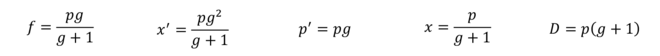
f  = p*g/(g+1)
x' = p*g^2/(g+1)
p' = p*g
x  = p/(g+1)
D  = p*(g+1)

Connaissant la focale et l’allongement, on obtient :

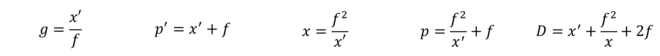
g  = x'/f
p' = x'+f
x  = f^2/x'
p  = f^2/x'+f
D  = x'+f^2/x'+2*f

Connaissant la focale et le tirage, on obtient :

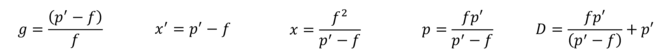
g  = (p'-f)/f
x' = p'-f
x  = f^2/(p'-f)
p  = f*p'/(p'-f)
D  = f*p'/(p'-f)+p’

Connaissant la focale et la distance de l’objet au plan focal image, on obtient :

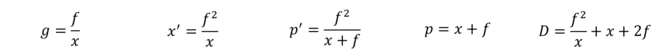
g  = f/x
x' = f^2/x
p' = f^2/x+f
p  = x+f
D  = f^2/x+x+2*f

Connaissant la focale et la distance de l’objet au centre optique, on obtient :

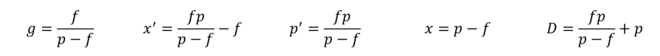
g  = f/(p-f)
x' = f*p/(p-f)-f
p' = f*p/(p-f)
x  = p-f
D  = f*p/(p-f)+p

Connaissant la focale et la distance de l’objet à l’image, on obtient :

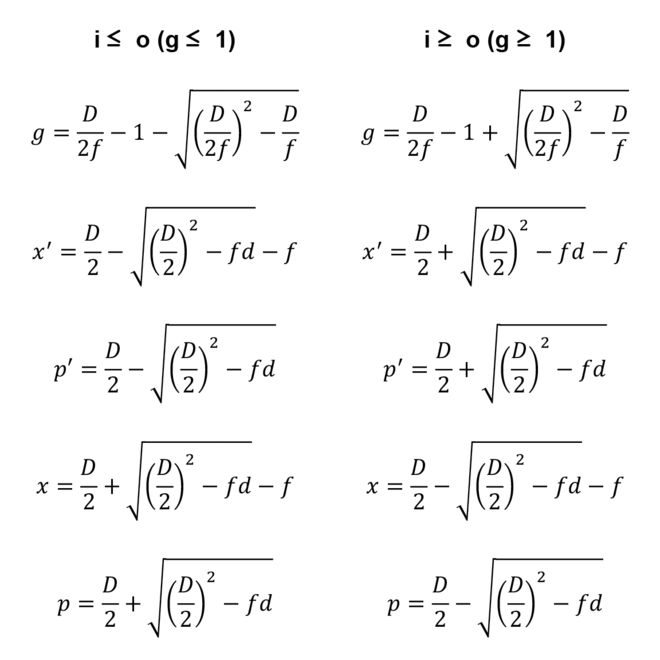
Pour i ≤ o (g ≤ 1) :

g  = D/(2*f)-1-RACINE((D/(2*f))^2-D/f)
x' = D/2-RACINE((D/2)^2-f*D)-f
p' = D/2-RACINE((D/2)^2-f*D)
x  = D/2+RACINE((D/2)^2-f*D)-f
p  = D/2+RACINE((D/2)^2-f*D)

Pour i ≥ o (g ≥ 1) :

g  = D/(2*f)-1+RACINE((D/(2*f))^2-D/f)
x' = D/2+RACINE((D/2)^2-f*D)-f
p' = D/2+RACINE((D/2)^2-f*D)
x  = D/2-RACINE((D/2)^2-f*D)-f
p  = D/2-RACINE((D/2)^2-f*D)

Profondeur de champ

Définitions

f	Distance focale
N	Ouverture relative
e	Diamètre du cercle de confusion
g	Grandissement (g = i / o)
x’	Tirage optique
h	Distance hyperfocale
p	Distance de mise au point
p₁	Premier plan net
p2	Dernier plan net

Diamètre du cercle de confusion

Exprime la tolérance de netteté, compte tenu du format. La valeur de 0,025 mm est souvent admise pour un format 24 × 36 mm ; cette valeur correspond à la diagonale du format divisé par 1730.

e = √(24²+36^²) / 1730 = 0,025

Profondeur de foyer

Limite arrière :

x’₁ = e N (g+1)² / (1 - e/f (g+1) N)

Limite avant :

x’₂ = e N (g+1)² / (1 + e/f (g+1) N)

Profondeur de foyer en fonction de g

Limite arrière :

p’₁ = f² (g+1) / (f - e (g+1) N)

Limite avant :

p’₂ = f² (g+1) / (f + e (g+1) N)

Profondeur de champ en fonction de g

Premier plan net :

p₁ = f² (1/g+1) / (f + e (1/g+1) N)

Dernier plan net :

p₂ = si(e f (1/g+1) N < f² ;
     f² (1/g+1) / (f - e (1/g+1) N) ; ∞)

Profondeur de champ en fonction de p

Premier plan net :

p₁ = p f² / (f² + e p N)

Dernier plan net :

p₂ = si (e p N < f² ; p f² / (f² - e p N) ; ∞)

Distance et ouverture en fonction des limites de la profondeur de champ

Distance :

p = 2 × p₁ × p₂ / (p1 + p2)

Ouverture :

N = f² / e / 2 (p₂ - p₁) / (p₁ × p₂)

Distance hyperfocale

h = f² / (e × N)

Propriétés de la distance hyperfocale

Distance de mise au point	Limite AV	Limite AR	Répartition AV	Répartition AR
∞	H	∞
h	h/2	∞
h/2	h/3	h	1/4	3/4
h/3	h/4	h/2	1/3	2/3
h/4	h/5	h/3	37,5%	62,5%
h/5	h/6	h/4	40%	60%
h/6	h/7	h/5	42%	50%
etc.

Limites de profondeur de champ en fonction de la distance de mise au point.

Profondeur de champ en fonction de la distance hyperfocale

Premier plan net :

p₁ = h × p / (h + p)

Dernier plan net :

p₂ = si(p < h ; h × p / (h - p) ; ∞)

Les distances h, p₁ et p₂ sont mesurées à partir du centre optique.

profondeur de champ = p₂ - p₁